How to Build a Mini Functor

Functors and monads. Both of them are useful and important design patterns in functional programming. More importantly, you can't understand monads without functors. So in this post, let's talk about functors. let's start with the definition of a functor.

What is a functor?

In case you don't know, a functor is actually not a thing originating from functional programming but from category theory, which is a branch of math. In category theory, a functor is a homomorphism between two categories. It probably sounds like nonsense at first, but please bear with me for a while, and I'll untangle this later so that you know what that means.

Let's familiar ourselves with a little category theory. It won't make you suffer so don't worry.

Categories

What is a category?

A category is basically a primitive abstracted structure, or a graph, with nodes and labeled directed edges. The nodes are called objects (not to confuse with objects in OOP), and the labeled directed edges are called arrows or morphisms or mappings. Notice that I draw a mapping in white and an object in black so that it's easier for you to tell them apart.

An object is a primitive structure in a category and has no properties. It only serves as the beginning and the end of a mapping. You don't have to be annoyed by the meaning of an object or a mapping here. They are just like quarks in physics, and you can't divide them further into smaller parts. A basic example of a category is the category of sets, where the objects are sets and the mappings are pure functions from one set to another. And for a loose definition, a set is just a bunch of things with something in common and that can be grouped together. In programming, in particular, you can think of sets as types, and mappings as pure functions. So from now on, when I say mapping or mappings, you can just think of them as pure functions.

A category has two basic abilities: the ability to compose the mappings, and the existence of an identity mapping for each object. Namely, the two most important properties of a category: composition and identity. In math, they look like these:

// Identity
id: X -> X
id(X) = X
// Identity Law
f ∘ id = id ∘ f = f
// Composition
(Y -> Z) ∘ (X -> Y) -> (X -> Z)

Visually, they look like these:

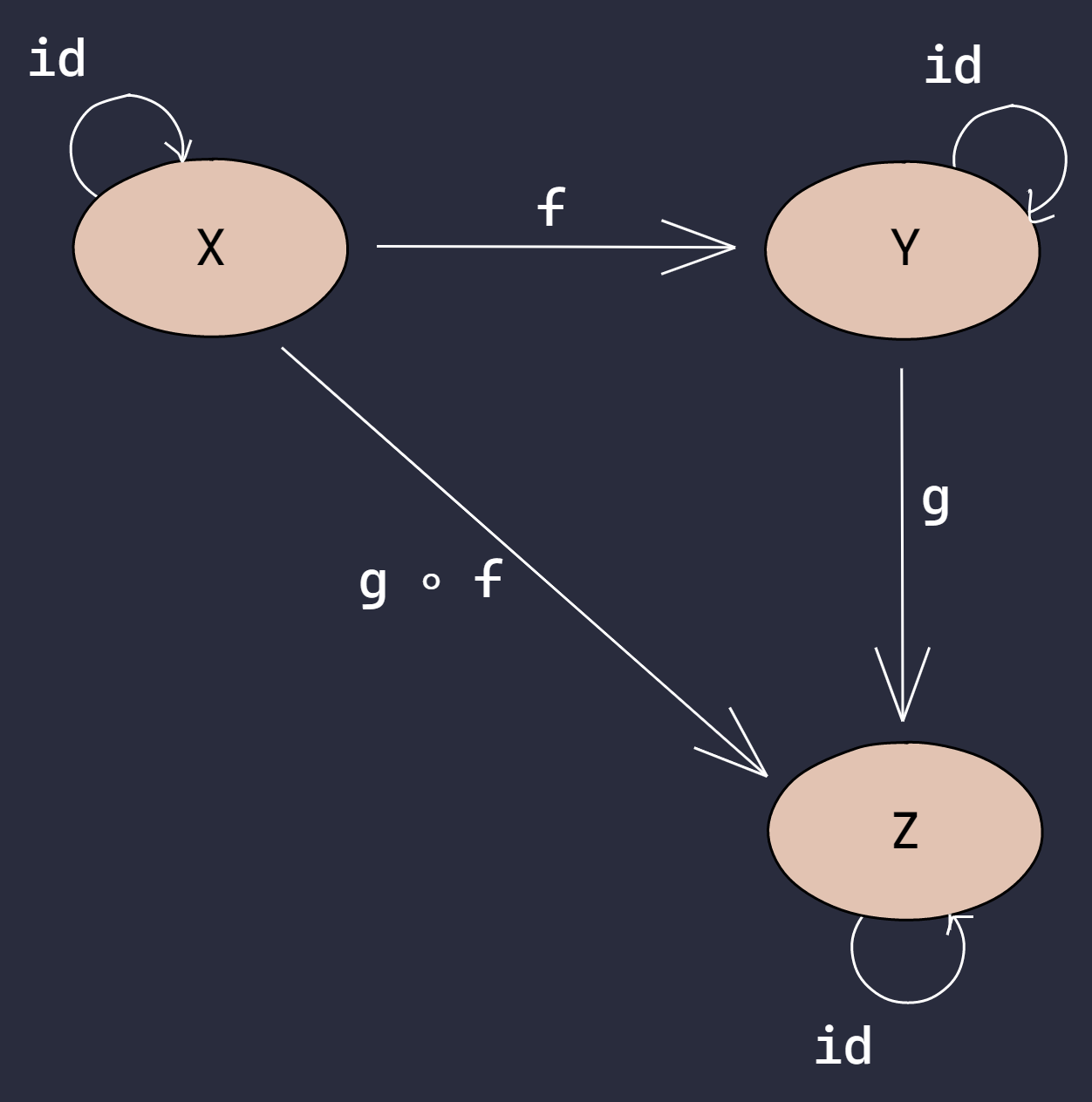
Notice that a category will have many mappings that take it to itself and the identity mapping is just a part of them and can be more than one.

Functors

You would discover functors yourself.

Category theory provides us with a way of formalizing generic abstract structures and patterns. And among those structures and patterns, so far, we have discovered and defined objects and mappings. But can we do more so that we have some more complex structures? As we mentioned before, a category consists of objects and mappings. What can we build on top of that? Well, we can have categories of categories and mappings between categories. By definition, objects have no structures. But categories definitely have structures, and therefore, by definition, if there are such things as mappings between categories, they need to preserve the structures of the categories. We can put it visually like this:

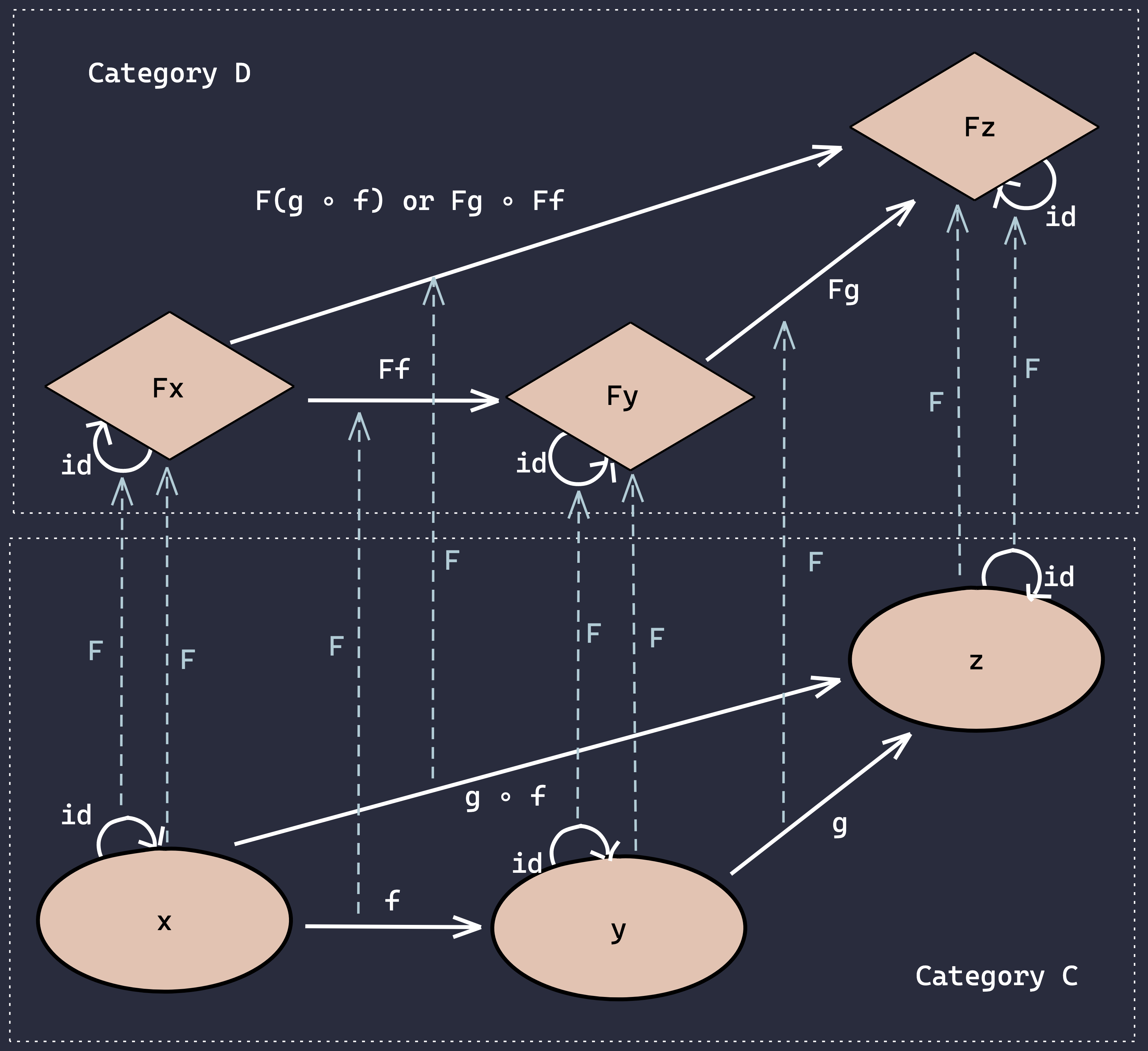
In this visualization, the categorical mapping F maps every object and mapping in category C into category D, including the mapping composition f ᐤ g and all identity mappings. So F is a functor, or a mapping from a category to another, preserving all existing objects, mappings, compositions, and identities. That is what we call homomorphism. "Homo" means "the same", so homomorphism means mappings that preserve structures.

Mathematicians often use diagrams to illustrate the properties of different kinds of mappings. The arrows inside categories are usually horizontal, while the arrows between categories, i.e. functors, are vertical (going up). That’s why the mappings of functors are often called lifting. You can take a function operating on integers and “lift it” (using a functor) to a function operating on lists of integers, and so on.

Now you know what a functor really means, how do we benefit from it while programming? Functor provides us with a better way to do function composition. Why? Because functors are mappings, and mappings can be composed.

Let's create a simple functor mapping (function) for me to demonstrate this.

const Functor = (x) => ({
  map: (f) => Functor(f(x)),
  value: x,
})

const number = Functor(0)

Here is an extremely simple functor, which has a .map method that can be used to map a function over a Functor. It also has a .value property, which can be used to extract its value. It obeys the two functor laws: composition law and identity law.

// Composition Law
const f = (x) => x + 1
const g = (x) => x * 2
number.map(f).map(g).value === number.map((x) => g(f(x))).value // true
// Identity Law
number.map((x) => x).value === number // true

And here is how we use it.

const nextCharForNumberString = (str) =>
  Functor(str)
    .map((str) => str.trim())
    .map((trimmed) => parseInt(trimmed))
    .map((number) => new Number(number + 1))
    .map((nextNumber) => String.fromCharCode(nextNumber)).value

const result = nextCharForNumberString(' 41 ')
console.log(result) // '*'

If you were to write it the procedural way, it might look like this, which is much harder to read and reason about especially when it gets more complicated:

const nextCharForNumberString_ = (str) => {
  const trimmed = str.trim()
  const number = parseInt(trimmed)
  const nextNumber = new Number(number + 1)
  return String.fromCharCode(nextNumber)
}

You have to trace the procedures one by one using your eyesight and it's so easy for you to lose track of the procedure. Or you can do the regular function composition the basic way, but it's even harder to read than the one in the non-functional style since you have to define every step as a small function, compose them together using the compose method, and read them from the end to the beginning. It's too much trouble. So obviously, functors are your best choice when you want to use function composition with a big workload. But of course, when you want a functor to be able to apply a function over a batch of data, you'll have to implement some kind of loop or recursion mechanism in the Functor so that all values can be mapped through that function.

We can further refactor this Functor by getting rid of the .value property and replace it with a better solution, like this:

const Functor = (x) => ({
  map: (f) => Functor(f(x)),
  fold: (f) => f(x),
})

The .fold method just applies the provided function to the value inside the Functor and returns it, which is more succinct than when we always have to do a .map and append a .value at the end. Why the name fold? Because it's kind like folding a box down to a single surface or dot. And it's a convention in the functional programming community, so let's just ride with it.

const nextCharForNumberString = (str) =>
  MyFunctor(str)
    .map((str) => str.trim())
    .map((trimmed) => parseInt(trimmed))
    .map((number) => new Number(number + 1))
    .fold((nextNumber) => String.fromCharCode(nextNumber))

Other Sweet Benefits of Functors

• Syntax unification: .map rather than nesting or compose
• Readable Composition: Left to right, human-readable order
• Statefulness: You can track it down through each step
• Separation of Concerns: You can extract function definitions away from a .map step
• Batch operation without loops: Saves you quite a lot of headaches.
• Safer and Cleaner: Works regardless of the context

Endofunctors

As I mentioned before, in programming we typically only deal with a single category consisting of all types (objects) and all functions (mappings). So the most commonly-seen functors are endofunctors. Some of you might recognize this word because you've seen the definition of a monad by Philip Wadler: "A monad is just a monoid in the category of endofunctors. What's the problem?" But actually, endofunctor is a pretty easy-to-understand concept. Just break the word into two parts. "endo-" means "inner", "functor" means "functor", so an endofunctor is just a functor that maps one category to itself. In the next post, we will continue this series by introducing the ultimate, glorious MONAD. The endofunctor is a good thing to know, but it won't matter even if you don't understand it for you to use monad in your daily practice. Because in programming, almost every functor is an endofunctor. But if you do make sense of it, it would be the best.